BUFFER SOLUTIONS

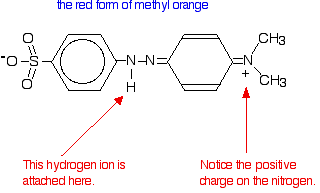
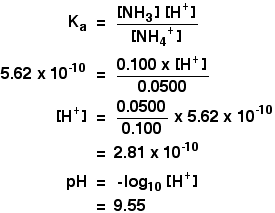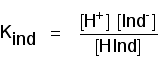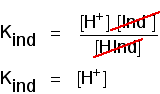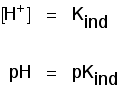This page describes simple acidic and alkaline buffer solutions and explains how they work.

What is a buffer solution?

Definition
A buffer solution is one which resists changes in pH when small quantities of an acid or an alkali are added to it.

Acidic buffer solutions

An acidic buffer solution is simply one which has a pH less than 7. Acidic buffer solutions are commonly made from a weak acid and one of its salts - often a sodium salt.

A common example would be a mixture of ethanoic acid and sodium ethanoate in solution. In this case, if the solution contained equal molar concentrations of both the acid and the salt, it would have a pH of 4.76. It wouldn't matter what the concentrations were, as long as they were the same.


You can change the pH of the buffer solution by changing the ratio of acid to salt, or by choosing a different acid and one of its salts.




Alkaline buffer solutions
An alkaline buffer solution has a pH greater than 7. Alkaline buffer solutions are commonly made from a weak base and one of its salts.
A frequently used example is a mixture of ammonia solution and ammonium chloride solution. If these were mixed in equal molar proportions, the solution would have a pH of 9.25. Again, it doesn't matter what concentrations you choose as long as they are the same.

How do buffer solutions work?
A buffer solution has to contain things which will remove any hydrogen ions or hydroxide ions that you might add to it - otherwise the pH will change. Acidic and alkaline buffer solutions achieve this in different ways.


Acidic buffer solutions
We'll take a mixture of ethanoic acid and sodium ethanoate as typical.
Ethanoic acid is a weak acid, and the position of this equilibrium will be well to the left:

Adding sodium ethanoate to this adds lots of extra ethanoate ions. According to Le Chatelier's Principle, that will tip the position of the equilibrium even further to the left.



The solution will therefore contain these important things:

• lots of un-ionised ethanoic acid;
• lots of ethanoate ions from the sodium ethanoate;
• enough hydrogen ions to make the solution acidic.

Other things (like water and sodium ions) which are present aren't important to the argument.


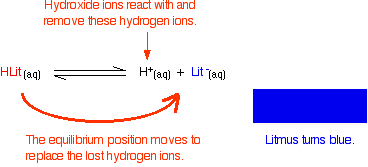
Adding an acid to this buffer solution
The buffer solution must remove most of the new hydrogen ions otherwise the pH would drop markedly.
Hydrogen ions combine with the ethanoate ions to make ethanoic acid. Although the reaction is reversible, since the ethanoic acid is a weak acid, most of the new hydrogen ions are removed in this way.

Since most of the new hydrogen ions are removed, the pH won't change very much - but because of the equilibria involved, it willfall a little bit.



Adding an alkali to this buffer solution
Alkaline solutions contain hydroxide ions and the buffer solution removes most of these.
This time the situation is a bit more complicated because there are two processes which can remove hydroxide ions.
Removal by reacting with ethanoic acid
The most likely acidic substance which a hydroxide ion is going to collide with is an ethanoic acid molecule. They will react to form ethanoate ions and water.





Because most of the new hydroxide ions are removed, the pH doesn't increase very much.
Removal of the hydroxide ions by reacting with hydrogen ions
Remember that there are some hydrogen ions present from the ionisation of the ethanoic acid.

Hydroxide ions can combine with these to make water. As soon as this happens, the equilibrium tips to replace them. This keeps on happening until most of the hydroxide ions are removed.

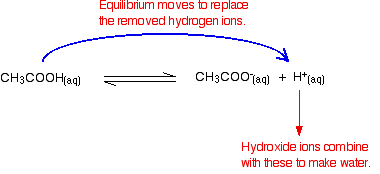
Again, because you have equilibria involved, not all of the hydroxide ions are removed - just most of them. The water formed re-ionises to a very small extent to give a few hydrogen ions and hydroxide ions.

Alkaline buffer solutions
We'll take a mixture of ammonia and ammonium chloride solutions as typical.
Ammonia is a weak base, and the position of this equilibrium will be well to the left:

Adding ammonium chloride to this adds lots of extra ammonium ions. According to Le Chatelier's Principle, that will tip the position of the equilibrium even further to the left.
The solution will therefore contain these important things:

• lots of unreacted ammonia;
• lots of ammonium ions from the ammonium chloride;
• enough hydroxide ions to make the solution alkaline.

Other things (like water and chloride ions) which are present aren't important to the argument.


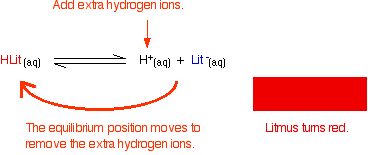
Adding an acid to this buffer solution
There are two processes which can remove the hydrogen ions that you are adding.
Removal by reacting with ammonia

The most likely basic substance which a hydrogen ion is going to collide with is an ammonia molecule. They will react to form ammonium ions.


Most, but not all, of the hydrogen ions will be removed. The ammonium ion is weakly acidic, and so some of the hydrogen ions will be released again.

Removal of the hydrogen ions by reacting with hydroxide ions
Remember that there are some hydroxide ions present from the reaction between the ammonia and the water.


Hydrogen ions can combine with these hydroxide ions to make water. As soon as this happens, the equilibrium tips to replace the hydroxide ions. This keeps on happening until most of the hydrogen ions are removed.

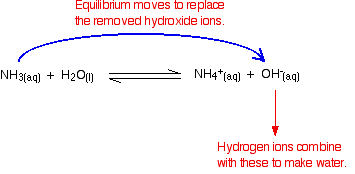
Again, because you have equilibria involved, not all of the hydrogen ions are removed - just most of them.


Adding an alkali to this buffer solution
The hydroxide ions from the alkali are removed by a simple reaction with ammonium ions.

Because the ammonia formed is a weak base, it can react with the water - and so the reaction is slightly reversible. That means that, again, most (but not all) of the the hydroxide ions are removed from the solution.

Acidic buffer solutions

This is easier to see with a specific example. Remember that an acid buffer can be made from a weak acid and one of its salts.

Let's suppose that you had a buffer solution containing 0.10 mol dm^-3 of ethanoic acid and 0.20 mol dm^-3 of sodium ethanoate. How do you calculate its pH?
In any solution containing a weak acid, there is an equilibrium between the un-ionised acid and its ions. So for ethanoic acid, you have the equilibrium:


The presence of the ethanoate ions from the sodium ethanoate will have moved the equilibrium to the left, but the equilibrium still exists.

That means that you can write the equilibrium constant, K_a, for it:


Where you have done calculations using this equation previously with a weak acid, you will have assumed that the concentrations of the hydrogen ions and ethanoate ions were the same. Every molecule of ethanoic acid that splits up gives one of each sort of ion.

That's no longer true for a buffer solution:


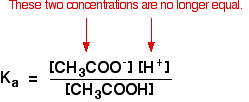
If the equilibrium has been pushed even further to the left, the number of ethanoate ions coming from the ethanoic acid will be completely negligible compared to those from the sodium ethanoate.

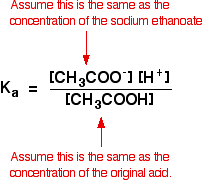
We therefore assume that the ethanoate ion concentration is the same as the concentration of the sodium ethanoate - in this case, 0.20 mol dm^-3.


In a weak acid calculation, we normally assume that so little of the acid has ionised that the concentration of the acid at equilibrium is the same as the concentration of the acid we used. That is even more true now that the equilibrium has been moved even further to the left.
So the assumptions we make for a buffer solution are:


Now, if we know the value for K_a, we can calculate the hydrogen ion concentration and therefore the pH.

K_a for ethanoic acid is 1.74 x 10^-5 mol dm^-3.

Remember that we want to calculate the pH of a buffer solution containing 0.10 mol dm^-3 of ethanoic acid and 0.20 mol dm^-3 of sodium ethanoate.

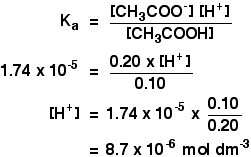
Then all you have to do is to find the pH using the expression  pH = -log₁₀ [H⁺]
You will still have the value for the hydrogen ion concentration on your calculator, so press the log button and ignore the negative sign (to allow for the minus sign in the pH expression).

You should get an answer of 5.1 to two significant figures. You can't be more accurate than this, because your concentrations were only given to two figures.

You could, of course, be asked to reverse this and calculate in what proportions you would have to mix ethanoic acid and sodium ethanoate to get a buffer solution of some desired pH. It is no more difficult than the calculation we have just looked at.
Suppose you wanted a buffer with a pH of 4.46. If you un-log this to find the hydrogen ion concentration you need, you will find it is 3.47 x 10^-5 mol dm^-3.

Feed that into the K_a expression.

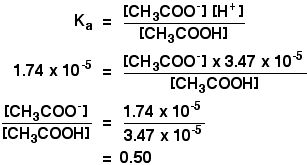
All this means is that to get a solution of pH 4.46, the concentration of the ethanoate ions (from the sodium ethanoate) in the solution has to be 0.5 times that of the concentration of the acid. All that matters is that ratio.


In other words, the concentration of the ethanoate has to be half that of the ethanoic acid.
One way of getting this, for example, would be to mix together 10 cm³ of 1.0 mol dm^-3 sodium ethanoate solution with 20 cm³of 1.0 mol dm^-3 ethanoic acid. Or 10 cm³ of 1.0 mol dm^-3 sodium ethanoate solution with 10 cm³ of 2.0 mol dm^-3 ethanoic acid. And there are all sorts of other possibilities.

Alkaline buffer solutions
We are talking here about a mixture of a weak base and one of its salts - for example, a solution containing ammonia and ammonium chloride.

The modern, and easy, way of doing these calculations is to re-think them from the point of view of the ammonium ion rather than of the ammonia solution. Once you have taken this slightly different view-point, everything becomes much the same as before.

So how would you find the pH of a solution containing 0.100 mol dm^-3 of ammonia and 0.0500 mol dm^-3 of ammonium chloride?

The mixture will contain lots of unreacted ammonia molecules and lots of ammonium ions as the essential ingredients.

The ammonium ions are weakly acidic, and this equilibrium is set up whenever they are in solution in water:


You can write a K_a expression for the ammonium ion, and make the same sort of assumptions as we did in the previous case:

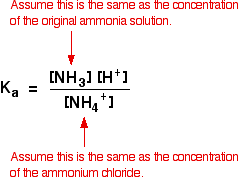
The presence of the ammonia in the mixture forces the equilibrium far to the left. That means that you can assume that the ammonium ion concentration is what you started off with in the ammonium chloride, and that the ammonia concentration is all due to the added ammonia solution.

The value for K_a for the ammonium ion is 5.62 x 10^-10 mol dm^-3.

Remember that we want to calculate the pH of a buffer solution containing 0.100 mol dm^-3 of ammonia and 0.0500 mol dm^-3 of ammonium chloride.
Just put all these numbers in the K_a expression, and do the sum:

ACID-BASE INDICATORS

This page describes how simple acid-base indicators work, and how to choose the right one for a particular titration.

How simple indicators work
Indicators as weak acids



Litmus
Litmus is a weak acid. It has a seriously complicated molecule which we will simplify to HLit. The "H" is the proton which can be given away to something else. The "Lit" is the rest of the weak acid molecule.
There will be an equilibrium established when this acid dissolves in water. Taking the simplified version of this equilibrium:





The un-ionised litmus is red, whereas the ion is blue.
Now use Le Chatelier's Principle to work out what would happen if you added hydroxide ions or some more hydrogen ions to this equilibrium.



Adding hydroxide ions:

Adding hydrogen ions:

If the concentrations of HLit and Lit ^- are equal:
At some point during the movement of the position of equilibrium, the concentrations of the two colours will become equal. The colour you see will be a mixture of the two.

The reason for the inverted commas around "neutral" is that there is no reason why the two concentrations should become equal at pH 7. For litmus, it so happens that the 50 / 50 colour does occur at close to pH 7 - that's why litmus is commonly used to test for acids and alkalis. As you will see below, that isn't true for other indicators.


Methyl orange
Methyl orange is one of the indicators commonly used in titrations. In an alkaline solution, methyl orange is yellow and the structure is:

Now, you might think that when you add an acid, the hydrogen ion would be picked up by the negatively charged oxygen. That's the obvious place for it to go. Not so!
In fact, the hydrogen ion attaches to one of the nitrogens in the nitrogen-nitrogen double bond to give a structure which might be drawn like this:

You have the same sort of equilibrium between the two forms of methyl orange as in the litmus case - but the colours are different.

You should be able to work out for yourself why the colour changes when you add an acid or an alkali. The explanation is identical to the litmus case - all that differs are the colours.




In the methyl orange case, the half-way stage where the mixture of red and yellow produces an orange colour happens at pH 3.7 - nowhere near neutral. This will be explored further down this page.


Phenolphthalein

Phenolphthalein is another commonly used indicator for titrations, and is another weak acid.

In this case, the weak acid is colourless and its ion is bright pink. Adding extra hydrogen ions shifts the position of equilibrium to the left, and turns the indicator colourless. Adding hydroxide ions removes the hydrogen ions from the equilibrium which tips to the right to replace them - turning the indicator pink.
The half-way stage happens at pH 9.3. Since a mixture of pink and colourless is simply a paler pink, this is difficult to detect with any accuracy!

The pH range of indicators
The importance of pK_ind
Think about a general indicator, HInd - where "Ind" is all the rest of the indicator apart from the hydrogen ion which is given away:

Because this is just like any other weak acid, you can write an expression for K_a for it. We will call it K_ind to stress that we are talking about the indicator.

Think of what happens half-way through the colour change. At this point the concentrations of the acid and its ion are equal. In that case, they will cancel out of the K_ind expression.

You can use this to work out what the pH is at this half-way point. If you re-arrange the last equation so that the hydrogen ion concentration is on the left-hand side, and then convert to pH and pK_ind, you get:

That means that the end point for the indicator depends entirely on what its pK_ind value is. For the indicators we've looked at above, these are:

indicator	pKind
litmus	6.5
methyl orange	3.7
phenolphthalein	9.3

The pH range of indicators
Indicators don't change colour sharply at one particular pH (given by their pK_ind). Instead, they change over a narrow range of pH.

Assume the equilibrium is firmly to one side, but now you add something to start to shift it. As the equilibrium shifts, you will start to get more and more of the second colour formed, and at some point the eye will start to detect it.

For example, suppose you had methyl orange in an alkaline solution so that the dominant colour was yellow. Now start to add acid so that the equilibrium begins to shift.
At some point there will be enough of the red form of the methyl orange present that the solution will begin to take on an orange tint. As you go on adding more acid, the red will eventually become so dominant that you can no longe see any yellow.

There is a gradual smooth change from one colour to the other, taking place over a range of pH. As a rough "rule of thumb", the visible change takes place about 1 pH unit either side of the pK_ind value.
The exact values for the three indicators we've looked at are:

indicator	pKind	pH range
litmus	6.5	5 - 8
methyl orange	3.7	3.1 - 4.4
phenolphthalein	9.3	8.3 - 10.0

The litmus colour change happens over an unusually wide range, but it is useful for detecting acids and alkalis in the lab because it changes colour around pH 7. Methyl orange or phenolphthalein would be less useful.
This is more easily seen diagramatically.

For example, methyl orange would be yellow in any solution with a pH greater than 4.4. It couldn't distinguish between a weak acid with a pH of 5 or a strong alkali with a pH of 14.

Choosing indicators for titrations
Remember that the equivalence point of a titration is where you have mixed the two substances in exactly equation proportions. You obviously need to choose an indicator which changes colour as close as possible to that equivalence point. That varies from titration to titration.

Strong acid v strong base
The next diagram shows the pH curve for adding a strong acid to a strong base. Superimposed on it are the pH ranges for methyl orange and phenolphthalein.

You can see that neither indicator changes colour at the equivalence point.

However, the graph is so steep at that point that there will be virtually no difference in the volume of acid added whichever indicator you choose. However, it would make sense to titrate to the best possible colour with each indicator.

If you use phenolphthalein, you would titrate until it just becomes colourless (at pH 8.3) because that is as close as you can get to the equivalence point.

On the other hand, using methyl orange, you would titrate until there is the very first trace of orange in the solution. If the solution becomes red, you are getting further from the equivalence point.

Strong acid v weak base

This time it is obvious that phenolphthalein would be completely useless. However, methyl orange starts to change from yellow towards orange very close to the equivalence point.
You have to choose an indicator which changes colour on the steep bit of the curve.

Weak acid v strong base

This time, the methyl orange is hopeless! However, the phenolphthalein changes colour exactly where you want it to.

Weak acid v weak base
The curve is for a case where the acid and base are both equally weak - for example, ethanoic acid and ammonia solution. In other cases, the equivalence point will be at some other pH.

You can see that neither indicator is any use. Phenolphthalein will have finished changing well before the equivalence point, and methyl orange falls off the graph altogether.
It may be possible to find an indicator which starts to change or finishes changing at the equivalence point, but because the pH of the equivalence point will be different from case to case, you can't generalise.

On the whole, you would never titrate a weak acid and a weak base in the presence of an indicator.

Sodium carbonate solution and dilute hydrochloric acid
This is an interesting special case. If you use phenolphthalein or methyl orange, both will give a valid titration result - but the value with phenolphthalein will be exactly half the methyl orange one.

It so happens that the phenolphthalein has finished its colour change at exactly the pH of the equivalence point of the first half of the reaction in which sodium hydrogencarbonate is produced.

The methyl orange changes colour at exactly the pH of the equivalence point of the second stage of the reaction.